Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the mass and the center of mass of the lamina occupying the region R,where R is the triangular region with vertices 
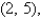 and
and 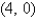 ,and having the mass density
,and having the mass density 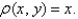
A) ![]()
![]() ,
, ![]()
B) ![]()
![]() ,
, ![]()
C) ![]() ,
, ![]()
D) ![]() ,
, ![]()
F) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the volume under 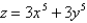 and above the region bounded by
and above the region bounded by 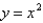 and
and 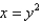 .
.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Short Answer
Sketch the solid whose volume is given by the iterated integral 
Correct Answer

verified
Correct Answer
verified
Short Answer
The double integral 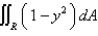 ,where
,where 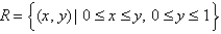 ,gives the volume of a solid.Describe the solid.
,gives the volume of a solid.Describe the solid.
Correct Answer

verified
The wedge bounded ab...View Answer
Show Answer
Correct Answer
verified
View Answer
Short Answer
Evaluate the integral by reversing the order of integration. 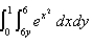
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Evaluate the double integral by first identifying it as the volume of a solid. 
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) A) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use polar coordinates to find the volume of the solid bounded by the paraboloid 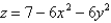 and the plane
and the plane 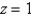 .
.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the center of mass of a lamina in the shape of an isosceles right triangle with equal sides of length 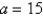 if the density at any point is proportional to the square of the distance from the vertex opposite the hypotenuse.Assume the vertex opposite the hypotenuse is located at
if the density at any point is proportional to the square of the distance from the vertex opposite the hypotenuse.Assume the vertex opposite the hypotenuse is located at 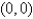 ,and that the sides are along the positive axes.
,and that the sides are along the positive axes.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) None of these
G) D) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use cylindrical coordinates to evaluate 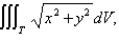 where T is the solid bounded by the cylinder
where T is the solid bounded by the cylinder  and the planes
and the planes 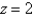 and
and 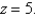
A) ![]()
![]()
B) ![]()
![]()
C) ![]()
![]()
D) ![]()
![]()
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the mass of a solid hemisphere of radius 5 if the mass density at any point on the solid is directly proportional to its distance from the base of the solid.
A) ![]() k
k ![]()
B) ![]() k
k ![]()
C) ![]() k
k ![]()
D) ![]() k
k ![]()
F) C) and D)
Correct Answer

verified
Correct Answer
verified
Short Answer
Use polar coordinates to evaluate. 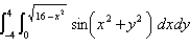
Correct Answer

verified
Correct Answer
verified
Short Answer
Identify the surface with equation 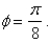
Correct Answer

verified
Upper half of a righ...View Answer
Show Answer
Correct Answer
verified
View Answer
Short Answer
Evaluate the double integral. 
 is bounded by the circle with center the origin and radius 36.
is bounded by the circle with center the origin and radius 36.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use a double integral to find the area of the region R where R is bounded by the circle 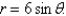
A) ![]()
![]()
B) ![]()
![]()
C) ![]()
![]()
D) ![]()
![]()
F) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Calculate the iterated integral. 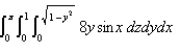
A) ![]()
B) ![]()
C) 8
D) ![]()
E) None of these
G) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the Jacobian of the transformation. 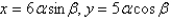
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) A) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use polar coordinates to find the volume of the sphere of radius 3 .Round to two decimal places.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) B) and D)
Correct Answer

verified
Correct Answer
verified
Short Answer
Evaluate 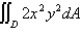 where D is the figure bounded by
where D is the figure bounded by 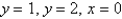 and
and  .
.
Correct Answer

verified
Correct Answer
verified
Short Answer
Calculate the double integral.Round your answer to two decimal places. 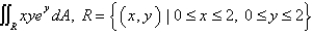
Correct Answer

verified
Correct Answer
verified
Showing 21 - 40 of 54
Related Exams