A)
B)
C)
D)
F) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find functions and such that . -
A)
B)
C)
D)
F) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -The total revenue from the sale of stereos is given by . Find the average revenue from the sale of stereos.
A)
B)
C)
D)
F) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the properties of limits to evaluate the limit if it exists. -
A)
B)
C)
D) Does not exist
F) C) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the derivative. -
A)
B)
C)
D)
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find and . -
A)
B)
C)
D)
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem.} -A car rental firm charged per day or portion of a day to rent a car for a period of 1 to 4 days. Days 5 to 8 were then "free," while the charge for days 9 through 15 was again per day. Let represent the total cost to rent the car for days, where 15 . Find the total cost of a rental for 3 days.
A)
B)
C)
D)
F) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find for the function, then find for the given . -
A)
B)
C)
D)
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the limit properties to find the following limit. -If and , find .
A) -1
B)
C)
D) Does not exist
F) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the equation of the tangent line to the curve when has the given value. -
A)
B)
C)
D)
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
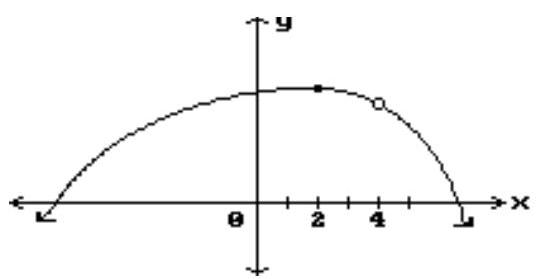
Find all points where the function is discontinuous.
-
A)
B)
C)
D) None
F) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -The cost of manufacturing a particular videotape (in dollars) is , where is the number of tapes produced. The average cost per tape (in dollars) , denoted by , is found by dividing by . Find .
A)
B)
C)
D) does not exist
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the point from those given that has the given property.
-The point where the slope of the tangent is least
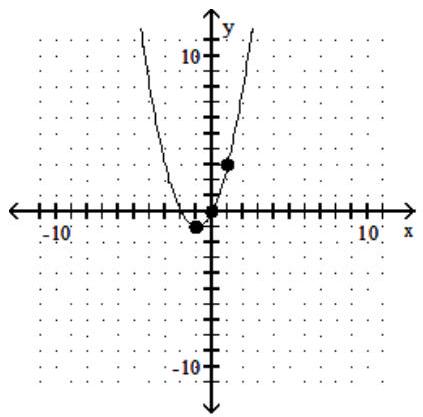
A)
B)
C)
E) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find and . -
A)
B)
C)
D)
F) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Provide the proper response. -A particle has a position function . Is the derivative of with respect to time at a given time , the average or instantaneous velocity?
A) A verage Velocity
B) Neither
C) I nstantaneous velocity
D) Both
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The graph shows the total sales in thousand of dollars from the distribution of x thousand catalogs. Find the average rate of change of sales with respect to the number of catalogs distributed for the change in x.
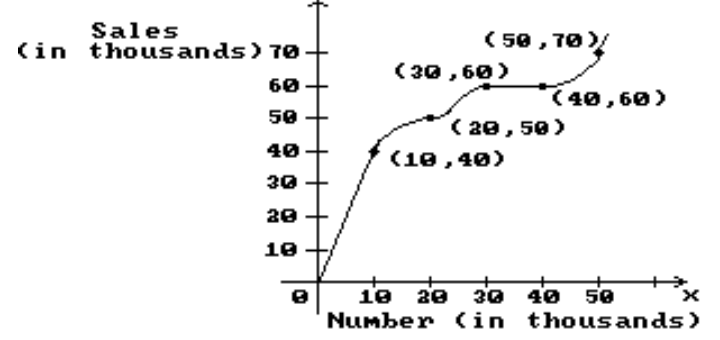 -10 to 30
-10 to 30
A) 3
B)
C)
D) 1
F) C) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Let and . Find the composite. -
A)
B)
C)
D)
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the equation of the tangent line to the curve when has the given value. -
A)
B)
C)
D)
F) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the following. - if
A) 96
B) 6
C) 8
D) 159
F) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the derivative. -
A)
B)
C)
D)
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Showing 301 - 320 of 342
Related Exams