A)
B)
C)
D)
E) None of these
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Essay
Find the center of mass of the lamina of the region shown if the density of the circular lamina is four times that of the rectangular lamina. 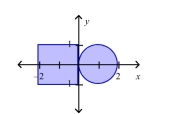
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Calculate the double integral.
A) 250
B) 230
C) 190
D) 180
E) 210
G) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Evaluate the double integral by first identifying it as the volume of a solid.
A) 300
B) -100
C) 0
D) 200
E) 100
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the given transformation to evaluate the integral. , where is the region in the first quadrant bounded by the lines and the hyperbolas .
A)
B)
C)
D)
E)
G) B) and D)
Correct Answer

verified
Correct Answer
verified
Short Answer
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use polar coordinates to find the volume of the solid under the paraboloid and above the disk .
A)
B)
C)
D)
E)
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Short Answer
Evaluate the integral by changing to polar coordinates. is the region bounded by the semicircle and the -axis.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Calculate the double integral.
A) 190
B) 170
C) 130
D) 150
E) 120
G) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Calculate the iterated integral.Round your answer to two decimal places.
A)
B)
C)
D)
E)
G) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the Jacobian of the transformation.
A)
B)
C)
D)
E)
G) A) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use cylindrical coordinates to evaluate , where is the solid bounded by the cylinder and the planes and .
A)
B)
C)
D)
F) B) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the area of the surface. The part of the surface that lies above the -plane.
A)
B)
C)
D)
E)
G) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Evaluate the double integral by first identifying it as the volume of a solid.
A) 40
B)
C)
D) 140
E) 240
G) All of the above
Correct Answer

verified
Correct Answer
verified
Essay
Sketch the solid bounded by the graphs of the equations and , and then use a triple integral to find the volume of the solid.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the center of mass of a lamina in the shape of an isosceles right triangle with equal sides of length if the density at any point is proportional to the square of the distance from the vertex opposite the hypotenuse. Assume the vertex opposite the hypotenuse is located at , and that the sides are along the positive axes.
A)
B)
C)
D)
E) None of these
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the Midpoint Rule with four squares of equal size to estimate the double integral.
A)
B)
C)
D)
E)
G) C) and E)
Correct Answer

verified
Correct Answer
verified
Short Answer
Calculate the iterated integral.
Correct Answer

verified
Correct Answer
verified
Short Answer
Calculate the iterated integral.
Correct Answer

verified
Correct Answer
verified
Short Answer
Use spherical coordinate to find the volume above the cone and inside sphere .
Correct Answer

verified
Correct Answer
verified
Showing 21 - 40 of 60
Related Exams